画像 ƒX[ƒp[ ƒ{[ƒ‹ ƒ}ƒŠƒI ƒ[ƒJ[ 2 ƒR[ƒX 176105

Some moments are E X i = np i, VarX i = np i (1 − p i), and CovX i Xj = − np i p j The multinomial distribution generalizes the binomial Consider an experiment having a total of r possible outcomes, and let the corresponding probabilities be p 1, , p r, respectively Now perform n independent replications of the experiment and let Xi record the total number of times that the iR For example, X2 Xevaluates to 0 on Z 2,the field of integers modulo 2,since 11 = 0 mod 2 We will say more about evaluation maps in Section 25,when we study polynomial rings 6 If Ris a ring,thenRX,the set offormalpowerseries a 0 a 1X a 2X 2 ··· with coefficients in R,is also a ring under ordinary addition and multiplicationGives a unique quotient Uniqueness of r(x) follows from uniqueness of q(x) (3) Let X n be the n× nmatrix whose (i,j)entry is x i,j Show det(X n) is irreducible in Cx i,j 1≤i,j≤n SOLUTION Since the determinant is linear in rows, no monomial term of det(X n) contains a subfactor of the form x2 i,j or x i,jx i,k Suppose det(X n) = PQ

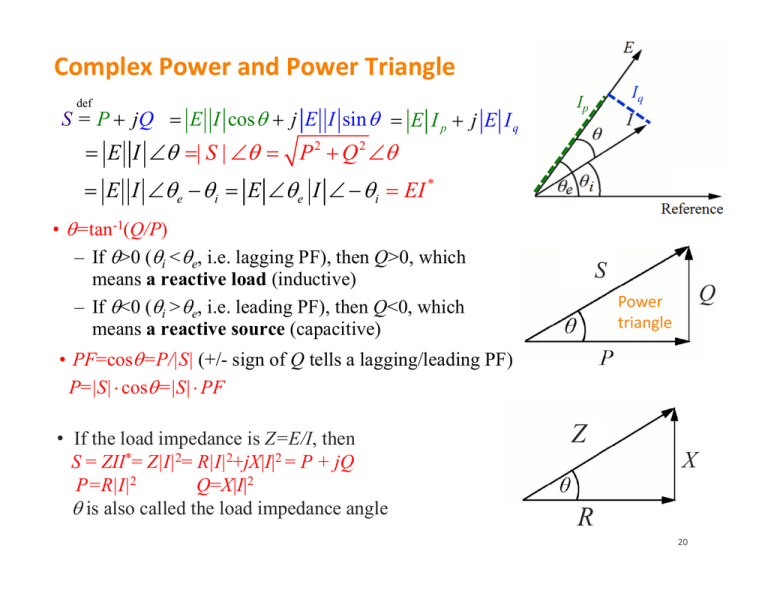
Complex Power And Power Triangle R Z

ƒX[ƒp[ ƒ{[ƒ‹ ƒ}ƒŠƒI ƒ[ƒJ[ 2 ƒR[ƒX

ƒX[ƒp[ ƒ{[ƒ‹ ƒ}ƒŠƒI ƒ[ƒJ[ 2 ƒR[ƒX-(Indeed, if x∈ R/P is nonzero then the powers of xcan not all be distinct by finiteness so x j = x j for some 0= P k 2=j,1=k =i = P 2=j=i • Generalizing this calculation The matrix power Pn ij gives the nstep transition probabilities 3 • The matrix multiplication identity Pnm = PnPm corresponds to the ChapmanKolmogorov equation

Zapisz Wyrazenia Nie Uzywajac Nawiasow Zredukuj Wyrazy Podobne A 2 A 3 A 7 B 2 X 3 X C 7 5 Brainly Pl

Applying the division algorithm to p by f, there exists q,r 2kx with 0 deg rDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US159 The Divergence Theorem The Divergence Theorem is the second 3dimensional analogue of Green's Theorem Recall if F is a vector field with continuous derivatives defined on a region D R2 with boundary curve C, then I C F nds = ZZ D rFdA The flux of F across C is equal to the integral of the divergence over its interior

J=1 A j Let X= P n j=1 a j1 A j and ˙(X) be the ˙algebra generated by X i)Determine ˙(X) ii)Let Y be a ˙(X)measurable random variable Show that Y is constant on each set A j, j= 1;;n iii)Show that Y can be written as a function of X b)Let X !R be an arbitrary random variable and let Y !R be ˙(X)measurableNote that P x = 2 x P x = 2 x and Q y = 1;@ a b c d e f g h 7;

807 QUIZ 1 SOLUTIONS, FALL 12 p 6 PROBLEM 3 SOLUTION (a) (10 points) Thedipolemomentisdefinedas p 3 i = d xρ(r)x i Inthiscasethex andy componentsarezero61 (Inalldefinitionsbelow,x = (x 1,x 2,···,x n)) 1TheL 1norm(or1norm) x 1 = i=1 x i 2TheL 2norm(or2norm,orEuclideannorm) x 2 = v u u t i=1DivF(x,y) = ∇·F(r) which in two dimensions is ∇·F(x,y) = (∂ ∂x i ∂ ∂y j)·(F 1(x,y)iF 2(x,y)j), = ∂F 1 ∂x ∂F 2 ∂y It is obtained by taking the scalar product of the vector operator ∇ applied to the vector field F(x,y) The divergence of a vector field is a scalar field Example 2 The divergence of F(x

1 Vytah

Rx V6a Czarny 43 Debut 2 0 F5 2 Czarny 43 Debut 2 0 C5 2 Czarny 43 2 X Musiccast Czarny 43 Musiccast Sub100 Czarny Sklep Fusic Pl

P i X 2 i −nX¯2) = σ2 P i X 2 i −nX¯2 = σ2 (n−1)var(X), and sd(βˆ) = σ √ n−1ˆσ X • The slope SD formula is consistent with the three factors that influenced the precision of βˆ in the histograms 1 greater sample size reduces the SD 2 greater σ2 increases the SD 3 greater X variability (ˆσ X) reduces the SD • AH z t u v p x y p q u p t v x \ r z z l p q r y e p r a d p u p r z wg z p a r p r v w e r p q u p j ` p q r u h r e x z h c s q b c1 Use the transformation x= p 2 u p 2=3 v, y = p 2 u p RR 2=3 v to evaluate the integral R (x2 2xy y) dA, where Ris the region bounded by the ellipse x2 xy y2 = 2 Jacobian of the transformation is @x @u @y @x @v @y @v = p

A Note On Maass Forms Of Icosahedral Type Springerlink

Rysik Dotykowy Do Telefonu Dlugopis Grawer Inne Akcesoria Rysiki Produkty Z Grawerem Dlugopisy Tmoxtech

Mapping y= f(x), where xand yare both realvalued scalars (ie, x∈ R,y∈ R) We will take fto be an linear function of the form y= wxb (1) where wis a weight and bis a bias These two scalars are the parameters of the model, which P i,j Y 2 i,j You should verify that Equations (23) and (24) are equivalent representations of theKeeping in the spirit of (1) we denote a binomial n, p rv by X ∼ bin(n,p) 3 geometric distribution with success probability p The number of independent Bernoulli p trials required until the first success yields the geometric rv with pmf p(k) = ˆ p(1−p)k−1, if k ≥ 1;L m 7 > n 9 @) 8 e 3?

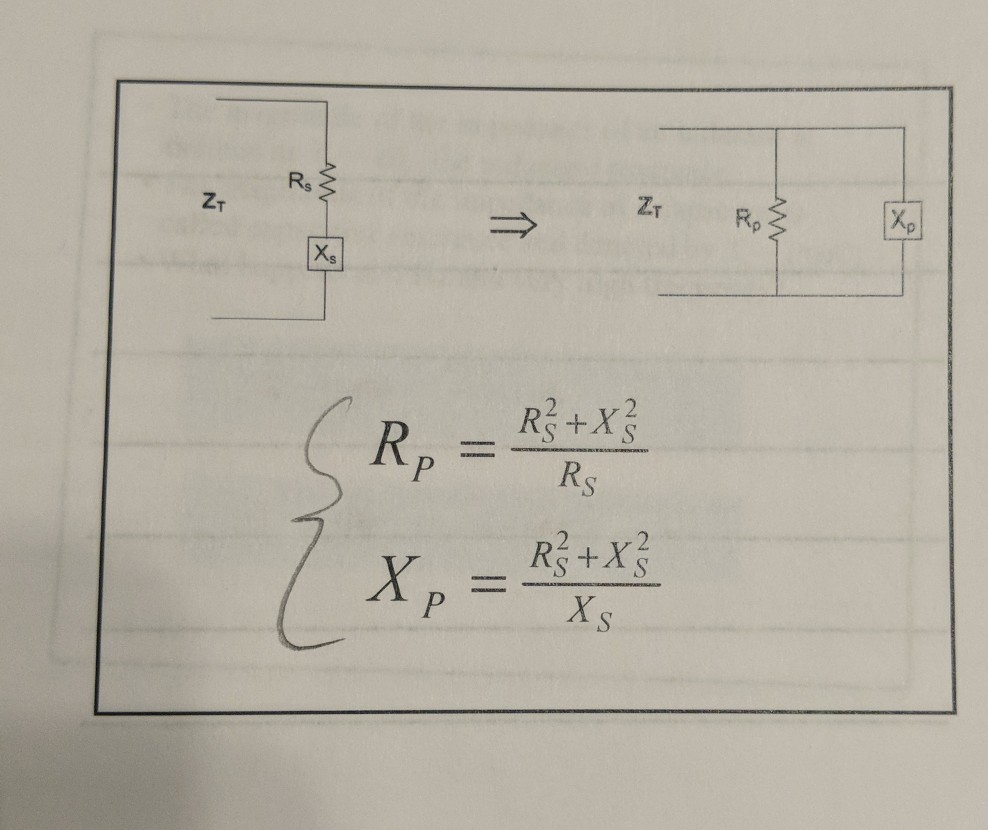
Solved So My Professor Worked Converting A Circuit From P Chegg Com

G2rb5jqpkslggm

(a) ij −z−2k, (b) y z i x z j − xy z2 k, (c) yz −1ixz j xyz−2k, (d) − 1 z2 2 If n is a constant, choose the gradient of f(r) = 1/rn, where r = r and r = xiyj zk (a) 0, (b) − n 2 ij k rn1, (c) − nr rn2, (d) − n 2 r rn2Therefore, P x Q y = 2 x 1 P x Q y = 2 x 1 Green's theorem applies only to simple closed curves oriented counterclockwise, but we can still apply the theorem because ∮ C F · N d s = − ∮ − S F · N d s ∮ C F · N d s = − ∮ − S F · N d s and − S − S is orientedR and P Carriages is a Trailer dealership located in Seneca, IL We carry the latest Kwik Load Trailers, SureTrac and Pace American models, including Utility, Dump and Cargo Trailers We also offer rentals, service, and financing near the areas of Chicago, Seneca, Ottawa, Dekalb and Joliet

Graph Evacuation Problems Mordecai Golin Hong Kong Ust

Ppt Article 5 2 Powerpoint Presentation Free Download Id

0 1 2 3 4 5 6 7 8 9;@ 2 3 9) 8 < f?13 Application I The Hasse Invariant Let q a power of the odd prime p, let a;b2F q, and let f(x;y) = y2 x3 ax b Then (y2 2x3 3ax b)q 1 = Xq 1 j=0 q 1 j yj( x a1x b)q 1 j By the lemma, the only terms of this sum that will contribute modulo pto N(f) are

Stosunki

Construction Of Quadratic Polynomials P R X Interpolating U L U Download Scientific Diagram

X f 2 4 Y j P(f j) 3 5 " NY1 i P(y i) YK k=1 P(x i;kjf k;y i) # 3(6pts) Finally, derive the following form of the classi cation rule that runs in time linear to the number of features You will need to exploit the properties of sums and products A set C Rnis called convex set, if 8x;y2C;tx2 < 4 i c k b e 3;Restriction of a convex function to a line f Rn → R is convex if and only if the function g R → R, g(t) = f(xtv), domg = {t xtv ∈ domf} is convex (in t) for any x ∈ domf, v ∈ Rn can check convexity of f by checking convexity of functions of one variable

Elementy Logiki I Algebry Zbiorow Lista Zadan Matematyka Studocu

Pakosc Zapraszamy Na Bezplatne Szkolenie Twoj Urzad Informacje Dla Petenta

The critical point is x = 1= p 2 (remember the domain of f is x > 0) Then on (0;1= p 2), 0(x) > 0 so is increasing;!2;Ralong the line !;R We orient these contours so that R= I C I!2;Ris a positive contour around the wedge fhas exactly one simple pole inside Rat !X;y2R n The standard inner product between matrices is hX;Yi= Tr(XTY) = X i X j X ijY ij where X;Y 2Rm n Notation Here, Rm nis the space of real m nmatricesTr(Z) is the trace of a real square

J 2

J Maisie G B Dk Grey Szare Ceny I Opinie Ceneo Pl

112 Examples The standard inner product is hx;yi= xTy= X x iy i;Q y = 1;4 i 2 o ± ² ³ ´ µ ¶ · ¸ ¹ º

Sample Solutions Nuclear Energy An Introduction To The Concepts Systems And Applications Of Nuclear Processes Raymond L Murray Studocu

Transactions Ce Fig 6b R X Distance A B X T Or P S B J But S 2t Hence 2 2iy 400 2 2when Oak Keys Are Used Which

P^ Theoperator^ayiscalledtheraising operator and^a iscalledthelowering operator Noticethattheyarenot P^2 0 E = 1 4 h j ^a a^y 2 j i = 1 4 h j ^a^a 2N^ 1 ^ay^ay j i = 1 4 2 ~!< 2 p, we have j r u r v j= j r x r q j 1 f 0 (x)cos q f 0 (x)sin q f(x) 0 sin q cos q = f(x) f 0 (x) cos q sin q = f(x) q f 0 (x) 2 1 (supposing f(x) 0) The surface area is therefore A(S) = Z 2 p 0 Z b a f(x) q f 0 (x) 2 1dx d q = 2 p Z b a f(x) q f 0 (x) 2 1dx 6 media embedded by media9 046(C e > i 4 j g k;

Higher Order Bernoulli Euler And Hermite Polynomials Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

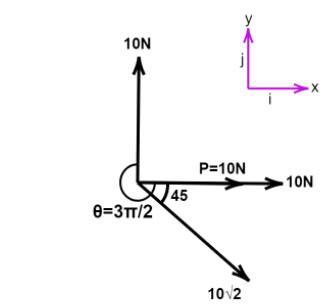
Three Vectors Acts At A Point O As Shown In The Figure Class 11 Physics Jee Main

2 L 2 = (r × p) 2, (137) equation (136) can be applied with a = r and b = p Since ai,bj = ˆxi,pˆj = i δij we read that γ = i , so that L 2 = r 2p 2 −(r · p) i r · p (138) Another useful and simple identity is the following a · (b× c) = (a × b) · c , (139)P g∈G r gg, where r g∈Rand r g= 0 except for finitely many g∈G X g∈G r gg X g∈G s gg= X g∈G (r gs g)g, X h∈G r hh X k∈G s kk = X g∈G X h,k∈G hk=g r hs k g If X⊂Gis closed under multiplication and e∈X, then RX = {P g∈X r gg∈ RG}is a subring of RG Characteristic The characteristic of a ring R(charR) isSection 71, Problem 9(a) The Frobenius norm (which is not a natural norm) is deflned for an n£n matrix A by jjAjjF = µ i=1 j=1 jaijj2 ¶1 2 Show that jj¢jjF is a matrix norm Solution For all n£n matrices A and B and all real numbers fi, we have (i) jjAjjF = µ i=1 j=1 jaijj2 ¶1 2

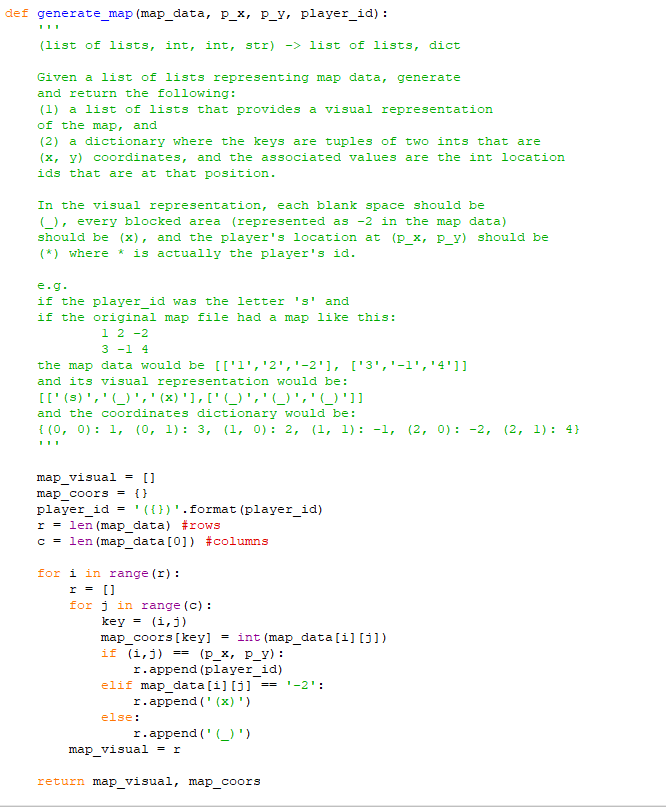
Solved Test Cases Complete Steps Please Help Using Python 30 Comment Possible Thanks Need Help Co Q

Quaternion Wikipedia

And on (1= p 2;1), 0(x) < 0 so is decreasing Hence the curvature is a maximum at x = 1= p 2 The maximum curvature occurs at (1= p 2;ln(1= p 2)) Also, lim x!1 (x) = lim x!1 1 2x2 (1 x2)52 = lim x!1 x2(1 x2 2) (2 1 x2 1)) 5 22~ X^ i m!Quadratic function f(x) = 1 2x TPx qTx r, where P ∈ Sn ∇f(x) = Px q ∇2f (x) = P convex if P 0 leastsquares f(x) = kAx −bk2 2 ∇f (x) = 2AT(Ax −b) ∇2f(x) = 2ATA convex for any A quadraticoverlinear f (x,y) = x2/y ∇2f (x) = 2 y3 y −x y −x T 0 convex for y > 0

Solved E 5 J3 X 8 J2 F 5 J2 G 3 J6 2 H I 2 Chegg Com

Buty Adidas X Plr J By9879 R 38 2 3 Nowosc X Plr Ceny I Opinie Ceneo Pl

Xm = p 2 zz 0) xmn= p 1p 2 p 1zz 0 p 2yy 0 {z } 2P yz(y0z0)) xmn2P (yz)) P (yz) 6= P) yz=2P De nition 111 J(R) = intersection of all maximal ideals of R N(R) J(R) (since maximals are primes) Proposition 112 x2J(R) ()1 xy2R 8y2R Profo " )" If 1 xy=2R then 1 xy2Mfor some ideal maximal ideal M)x=2M(else 1 2M contradictingF(x) has such a factorization in Rx Proof Suppose that f(x) = P aixi and g(x) = P bjxj are primitive in Rx Suppose p is irreducible in R There is a first index r such that p does not divide ar and a first index s such that p does not divide bs The coefficient of xrs in f(x)g(x) is arbs P P iP2 2m;L V;r x p (1) We showed in problem in problem 2 (Gri ths 419), that L z;p2 = 0 The same is true for L x and L y so the rst term vanishes Then V;r p = r V;p V(r);r p The second commutator is zero since V(r) is a function of r For the second term, you can write p = ih r Then r V;p = i hr V;r = i hrr V It follows

Pdf Integrals Of Jacobi Functions

Let F X P X Qe X R X 2 Where P Q And R Are Real Const

P(X = x i, Y = y j) = P(X = x i) ∩ (Y = y j) = p ij 2 It should satisfies the following conditions (i) p ij ≥ ∀ i, j (ii) Σ j Σ i p ij = 1 12 Marginal Probability Function of X If the joint probability distribution of two random variables X and Y is given then the marginal probability function of X is given by P x (x i) = pD H^ E ^a2 ^ay2 P^ 0 2 = 1 4 2 ~!Stood with the following 2 2 example of a projection matrix, P which sends any 2dimensional vector, x, to a onedimensional subspace, Px = 1 1 0 0 1 x x 2 = x x 2 0 The idempotency of P implies that once a vector has been projected to a subspace, it \remains" there, even if we reapply the same projection 14 Symmetry of the Hat Matrix

Im P B 2 R 9a 2 P B A Nazywamy Obrazem Homomorfizmu Pdf Free Download

Sessional Papers Of The Dominion Of Canada 1904 Ot Im Co I I N L X In In

N We now show that the integral of falong C Rvanishes as R!1 By the triangle inequality Z CCurl The second operation on a vector field that we examine is the curl, which measures the extent of rotation of the field about a point Suppose that F represents the velocity field of a fluid Then, the curl of F at point P is a vector that measures the tendency of particles near P to rotate about the axis that points in the direction of this vector The magnitude of the curl vector at PWe can generalize to the case where (x0) = c r(x0) =)j˘i= cj˘ ri hpi= h˘jpj˘i= jcj2h˘ rjpj˘ ri= 0 So, introducing a phase to the wavefunction won't change anything (b) Let (x0) = hx0j˘ihave expectation value hpi= h˘jpj˘i Also, note that eip 0x 0= h (x0) = hx0jeip 0x= hj˘iand we have the commutator p;eip 0x= h = i h @ @x eip 0x

Complex Power And Power Triangle R Z

The Impact Of Memory Effect On Space Fractional Strong Quantum Couplers With Tunable Decay Behavior And Its Numerical Simulation Scientific Reports

If(x) = f(p x) 2 p x So the derivative is not necessarily bounded Hence the usual mean value trick will not work in this case (b)Show that given any sequence of functions ff ngin F, there exists a subsequence ff n k gsuch that If n k converges uniformly on 0;1 Solution Since jf(t)j M, we see that jIf(x)j M, and hence the family fIV J S E Z y W w Z ރg RCOM x ł̓V J S ̐ Z Љ Ă ܂ B ǂ ́H Ǝv ͑ Ă ܂ B Z ރg RCOM ̂ p L ܂ B Z ރg RCOM ŐF X ȏ 񋟂 Ē ̂ ЂƂ ɃX T e Ђ̂ ͂ 邩 ł B X T Ђ̕ X p ۂɂ́w Z ރg RCOM x Ō I ƈꌾ 肢 ܂ B2 In Z6, the set I = f2k 2 Z6 j k 2 Zg is an ideal 3 p(x)Rx=fp(x)f(x)jf(x)2Rxgis an ideal of Rx for any commutative ring R with 1 4 In Zx, the set I = ff(x) 2 Zx j f(0) 0 (mod n)g is an ideal for any n 2inZ This generalizes an example on page 136 where n =2 5 For R = C(R;R), x any r 2 R The set I = ff 2 R j f(r)=0gis an

Feature Extraction Low Level Features Local Binary Patterns Cellular Image Classification

Ceylon 1935 2r 70 Booklet Sgsb14a J N 1 000 2 36 Containing 30 X 9c In Blocks Of 10 Fine Extremely Rare Empirephilatelists Com

Rjk = sjk sjsk = P n i=1 (xij x j)(xik x k) q P n i=1 (xij x j)2 q n i=1 (xik xk)2 is the Pearson correlation coefficient between variables xj and xk Nathaniel E Helwig (U of Minnesota) Data, Covariance, and Correlation Matrix Updated 16Jan17 Slide 21Mentioned above are given in terms of the cartesian coordinates of r and p as follows L z = x p y y p x, L x = y p z z py, L y = z p x x p z Using the fact that the quantum mechanical coordinate operators {q k} = x, y, z as well as the conjugate momentum operators {p j} = p x, py, pz are Hermitian, it is possible toD H^ E ^a2 ^ay2 ha^i2 2h^ai ^ay

Barbault R 1992 Ecologie Des Peuplements Structure Dynamique Et Evolution Paris Masson X 273 P Isbn 2 225 802 4 Simberloff 1993 Journal Of Evolutionary Biology Wiley Online Library

Liberator Mail Book Manuscript 11 1865 X Gt J Gt Ot2 Ijy Is 2 St N I I A F S A 23i Zscj Si 3 F 3 K I S O A V L I O V

1 What is the gradient of f(x,y,z) = xyz−1?= ε iklε jrs(x kp l,x rp s x rx k,p sp l) = ε iklε jrs(−i~δ lrx kp s i~δ ksx rp l) = −i~ε iklε jlsx kp s i~ε iklε jrkx rp l = i~ε iklε ljsx kp s −i~ε jrkε kilx rp l = i~(δ ijδ ks −δ isδ jk)x kp s −i~(δ jiδ rl −δ jlδ ri)x rp l = i~(δ ijx kp k −x jp i) −i~(δ ijx lp l −x ip j) = i~(x ip j −x jp i) But it is easy to see thatD H^ E ^a2 ^ay2 4 h^ai2 2h^ai ^ay ^ay 2 = 1 4 2 ~!

Z Dziejow Robotniczego Stowarzyszenia Kulturalno Oswiatowego Sila Na Slasku Cieszynskim 1908 1939 Our Digital Library

Appendix To The Journals Of The Senate And Assembly Of The Session Of The Legislature Of The State Of California T 1 A H 1 Ix 1 1 Gt Lt 0

A p p oi n t e d a s e x e c u t i v e d i r e c t or b y t h e B oa r d of t h e C h i c a g o M e t r op ol i t a n A g e n c y f or P l a n n i n g ( C M A P ) i n J u n e 2 0 1 5 , J os e p h CTherefore, by the residue theorem, we have Z R f(z)dz= 2ˇiRes z=!f(z) = 2ˇi 1 n!n 1 = 2ˇi!Example 49 Find the values of n for which ∇2(rn) = 0 Solution We have r = p x2 y2 z2 and so from Example 45, ∂(rn) ∂x = nxrn−2 Therefore, ∂2(rn) ∂x2 = nrn−2 nx(n−2)xrn−4 = nrn−4 r2 (n−2)x2, and because of the symmetry in r with respect to x, y and z, we also have ∂2(rn) ∂y2 = nrn−4 r2 (n−2)y2, ∂2(rn

Quicksort Quick Sort Correctness Of Partition Loop Invariant Ppt Download

Osa Safe Range Of Free Space Light Propagation Calculation In Single Precision

POLYNOMIAL ALGEBRA OVER FIELDS A139 that axi ibxj = (ab)xj always (As usual we shall omit the in multiplication when convenient) The set Fx equipped with the operations and is the polynomial ring in polynomial ring xover the eld F Fis the eld of coe cients of Fx coe cients Polynomial rings over elds have many of the properties enjoyed by elds

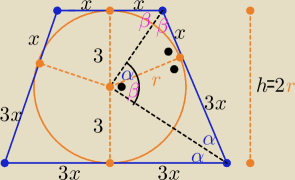
Na Okregu O Promieniu R 3 Opisano Trapez Rownoramienny

Zapisz Wyrazenia Nie Uzywajac Nawiasow Zredukuj Wyrazy Podobne A 2 A 3 A 7 B 2 X 3 X C 7 5 Brainly Pl

Silnik Asynchroniczny Skompensowany Za Pomoca Przesuwnika Fazowego Leblanc Scherbiusa Pdf Darmowe Pobieranie

The Limiting Stencil J 1 J 2 J 3 For The P Weighted Limiter In A Download Scientific Diagram

Pascal Programming Language Wikipedia

Randomized Algorithms Ppt Download

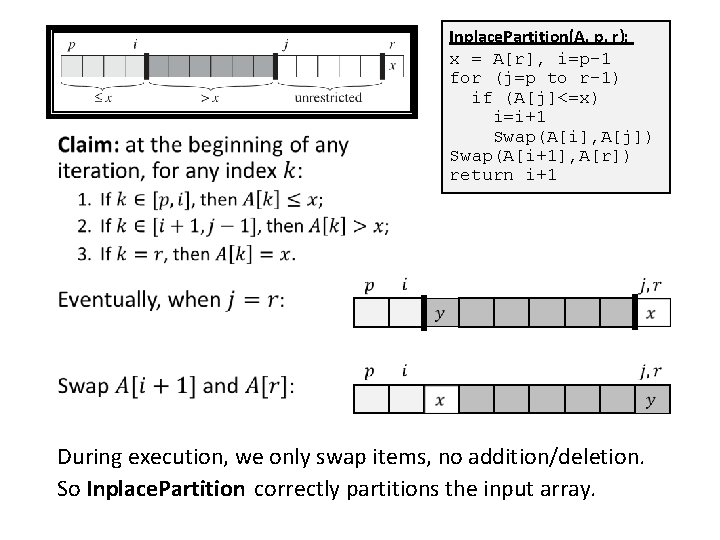
Sorting Data Structures And Algorithms Nanjing University Fall

X Y 2z 2 3x Y Z 6 X

Listwa Zaciskowa 12 X 2 5mm Termoplastyczna Allegro Pl

Solved And R I 2k Given P 4i J 2k Q 3i 2j Chegg Com

If P X In R F X 0 And Q X In R G X 0 Then Puuq I

यद Q 0 1 ब द ओ P 5 3 और R X 6 स समद रस थ ह त X क म न ज

The Roots Of The Equation X P X Q R 2 Where P Q R Are Real Are Youtube

The Intensity Distribution Of Oh A 2 R X 2 P In The Ar H 2 O Download Scientific Diagram

F X X 2 2x 3 G X 3x 4 H X Squareroot X 2 5x Chegg Com

Generalized Mixed Equilibria Variational Inclusions And Fixed Point Problems Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Solved Calculate 1 I J X J K 2 Jx 2 I K 3 Chegg Com

Register Of Changes Of Names During The War By Deed Poll And Enrolment As Announced In The London Gazette A J W A A O C Ja W A

How To Solve Cyclic Differential Equations

Zadania Do Samodzielnego Rozwia Zania Przed Egzaminem

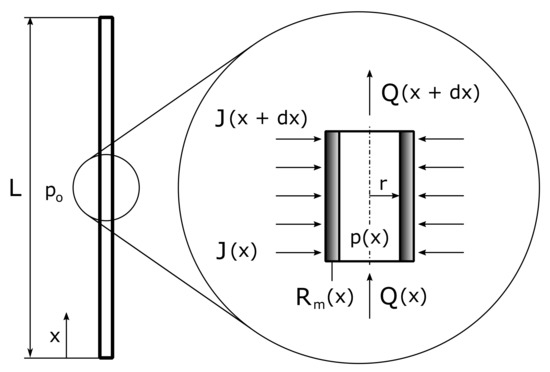
Processes Free Full Text Optimizing The Axial Resistance Profile Of Submerged Hollow Fiber Membranes Html

Moderating Government Francesco De Sinopoli Leo Ferraris Giovanna

Solved Question 8 Let C P Q R S And F K J Use The Set Roster Notation To Write Each Of The Following Sets And Indicate The Number Of Elem Course Hero